Intro to fp-ts, part 3: Option and Either

In the previous article we looked at the definition of a type class and touched concrete type classes like “functor”, “monad”, “monoid”. In this article I will describe how to work with nullable types and exceptions, so that the further presentation would be clearer when we move on to working with tasks and effects. Therefore, in this article, still aimed at beginning FP developers, I want to talk about a functional approach to solving some of the application problems that you have to deal with every day.

As always, I will illustrate the examples using data structures from fp-ts.

It has already become somewhat bad manners to quote Tony Hoare with his “billion-dollar mistake” — the invention of the concept of a null pointer in the ALGOL W language. This error, like a tumor, spread to other languages — C, C ++, Java, and, finally, JS. The possibility of assigning a variable of any type the null value leads to undesirable side effects when trying to access data by this pointer — the runtime throws an exception, so the code has to be coated with logic for handling such situations. I think you’ve all met (or even wrote) spaghetti code like this:

function foo(arg1, arg2, arg3) {
  if (!arg1) {
    return null;
  }

  if (!arg2) {
    throw new Error("arg2 is required")
  }

  if (arg3 && arg3.length === 0) {
    return null;
  }

  // finally business logic involving arg1, arg2, arg3 begins
}

TypeScript eliminates only a small part of this problem — with the strictNullChecks flag, the compiler prevents a non-nullable variable from being assigned the null value, throwing the TS2322 error. But at the same time, due to the fact that the type never is a subtype of all other types, the compiler does not restrict the programmer in any way from throwing an exception in an arbitrary part of the code. It turns out to be a ridiculous situation when you see the function add :: (x: number, y: number) => number in the public API of the library, but you cannot use it with certainty due to the fact that its implementation can throw an exception in the most unexpected place. In Java a class method can be marked with the keyword throws, which will oblige the caller to wrap the call in a try-catch statement or mark his method with a similar signature of the exception chain, but in TypeScript it’s hard to come up with anything other than (semi)useless JSDoc annotations for typing possible thrown exceptions.

It is also worth noting that the concepts of error and exception are often confused. I am fond of the convention adopted in the JVM world: Error is a problem from which there is no way to recover (say, the process is out of memory); exception is a special case of a program flow that needs to be handled (say, an overflow happened or an array came out of bounds). In the JS/TS world, we do not throw exceptions, but errors (throw new Error ()), which is a little confusing. In the following presentation, I will talk specifically about exceptions as entities generated by custom code and carrying very specific semantics — “an exception that it would be nice to handle.”

Today we will look how functional programming solves these two problems — “billion-dollar mistake” and exceptions.

`Option<A>` — a replacement for nullable types

In modern JS and TS it’s possible to use optional chaining and nullish coalescing for safe usage of nullable types. However, these syntactic constructions do not cover all needs of a programmer. Here’s an example of code, which cannot be rewritten using optional chaining — only using laborous work with if (a != null) {}, like in Go language:

const getNumber = (): number | null => Math.random() > 0.5 ? 42 : null;
const add5 = (n: number): number => n + 5;
const format = (n: number): string => n.toFixed(2);

const app = (): string | null => {
  const n = getNumber();
  const nPlus5 = n != null ? add5(n) : null;
  const formatted = nPlus5 != null ? format(nPlus5) : null;
  return formatted;
};

Enter Option<A> type! It could be understood as a container, which can be in two possible states: None in case of missing value, and Some in case of a presense of a value of type A:

type Option<A> = None | Some<A>;

interface None {
  readonly _tag: 'None';
}

interface Some<A> {
  readonly _tag: 'Some';
  readonly value: A;
}

It turned out that for such a structure, you can define instances of a functor, monad, and some other type classes. To cut down on the code, I’ll show you the implementation of the monad type class, and then we’ll draw parallels between the imperative code for handling null errors above and the functional-style code.

import { Monad1 } from 'fp-ts/Monad';

const URI = 'Option';
type URI = typeof URI;

declare module 'fp-ts/HKT' {
  interface URItoKind<A> {
    readonly [URI]: Option<A>;
  }
}

const none: None = { _tag: 'None' };
const some = <A>(value: A) => ({ _tag: 'Some', value });

const Monad: Monad1<URI> = {
  URI,
  // Functor part:
  map: <A, B>(optA: Option<A>, f: (a: A) => B): Option<B> => {
    switch (optA._tag) {
      case 'None': return none;
      case 'Some': return some(f(optA.value));
    }
  },
  // Applicative part:
  of: some,
  ap: <A, B>(optAB: Option<(a: A) => B>, optA: Option<A>): Option<B> => {
    switch (optAB._tag) {
      case 'None': return none;
      case 'Some': {
        switch (optA._tag) {
          case 'None': return none;
          case 'Some': return some(optAB.value(optA.value));
        }
      }
    }
  },
  // Monad/Chain part:
  chain: <A, B>(optA: Option<A>, f: (a: A) => Option<B>): Option<B> => {
    switch (optA._tag) {
      case 'None': return none;
      case 'Some': return f(optA.value);
    }
  }
};

As I wrote in the previous article, a monad allows you to organize sequential calculations. The interface of the monad type class is the same for different higher-kinded types — it consists of chain (aka bind or flatMap in other languages) and of (pure or return).

If JS/TS had syntactic sugar for easier work with the monadic interface, like in Haskell or Scala, then we would work consistently with nullable types, promises, code with exceptions, arrays and much more — instead of inflating the language with a large number of specific (and, often, only partial like in the case of optional chaining) solutions to particular cases (Promise/A +, then async/await, then optional chaining). Unfortunately, putting a mathematical foundation for the language is not a priority for the TC39 committee, so we take it of leave it.

Type Option is aleady available in the fp-ts module, so I’ll just import it from there, and rewrite the imperative example above in a functional style:

import { pipe, flow } from 'fp-ts/function';
import { option as O } from 'fp-ts';
import Option = O.Option;

const getNumber = (): Option<number> => Math.random() > 0.5 ? O.some(42) : O.none;
// we don't need to modify these functions, as they are already pure!
const add5 = (n: number): number => n + 5;
const format = (n: number): string => n.toFixed(2);

const app = (): Option<string> => pipe(
  getNumber(),
  O.map(n => add5(n)), // or just O.map(add5) via η-reduction
  O.map(format)
);

Due to the fact that functor laws imply preservation of function composition, we can rewrite app even shorter:

const app = (): Option<string> => pipe(
  getNumber(),
  O.map(flow(add5, format)),
);

N.B. In this tiny example, you don’t need to look at the business logic per se (it is deliberately made primitive), but it is important to note one thing about the functional paradigm as a whole: we did not just “use the function differently”, we abstract the general behavior for the computational context of the Option container (changing the value, if it’s present) from business logic (working with numbers). At the same time, the behavior itself transferred to the functor/monad/applicative/etc. can be reused in other places of the application, obtaining the same predictable sequence of calculations in the context of different business logic. We will look at how to do this in subsequent articles when we talk about Free Monads and the Tagless Final pattern. From my perspective, this is one of the strongest sides of the functional paradigm — abstracting away common things and then reusing them for composition into more complex structures.

`Either<E, A>` — computations that can diverge

Now let’s talk about exceptions. As I wrote above, an exceptional situation is a violation of the normal flow of execution of the program logic, which somehow needs to be responded to. At the same time, we do not have expressive means in the language itself — but we can get by with a data structure somewhat similar to Option, which is called Either:

interface Left<E> {
  readonly _tag: 'Left';
  readonly left: E;
}

interface Right<A> {
  readonly _tag: 'Right';
  readonly right: A;
}

type Either<E, A> = Left<E> | Right<A>;

The type Either <E, A> expresses the idea of a computation that can diverge in two ways: left, resulting with a value of type E, or right, resulting with a value of type A. Historically, there has been a convention in which the left path is considered the bearer of an erroneous data, and the right path is considered to be a successful outcome. For Either, you can implement many type classes — functor/monad/alternative/bifunctor/etc, and all this is already implemented in fp-ts/Either. As with Option, I will give the implementation of a monad for Either for general reference:

import { Monad2 } from 'fp-ts/Monad';

const URI = 'Either';
type URI = typeof URI;

declare module 'fp-ts/HKT' {
  interface URItoKind2<E, A> {
    readonly [URI]: Either<E, A>;
  }
}

const left = <E, A>(e: E) => ({ _tag: 'Left', left: e });
const right = <E, A>(a: A) => ({ _tag: 'Right', right: a });

const Monad: Monad2<URI> = {
  URI,
  // Functor:
  map: <E, A, B>(eitherEA: Either<E, A>, f: (a: A) => B): Either<E, B> => {
    switch (eitherEA._tag) {
      case 'Left':  return eitherEA;
      case 'Right': return right(f(eitherEA.right));
    }
  },
  // Applicative:
  of: right,
  ap: <E, A, B>(eitherEAB: Either<(a: A) => B>, eitherEA: Either<A>): Either<B> => {
    switch (eitherEAB._tag) {
      case 'Left': return eitherEAB;
      case 'Right': {
        switch (eitherEA._tag) {
          case 'Left':  return eitherEA;
          case 'Right': return right(eitherEAB.right(eitherEA.right));
        }
      }
    }
  },
  // Monad:
  chain: <E, A, B>(eitherEA: Either<E, A>, f: (a: A) => Either<E, B>): Either<E, B> => {
    switch (eitherEA._tag) {
      case 'Left':  return eitherEA;
      case 'Right': return f(eitherEA.right);
    }
  }
};

Let’s look at an example of imperative code that throws exceptions and rewrite it in a functional style. The classic example in which Either is demonstrated is validation. Suppose we are writing a new account registration API that accepts user email and password and checks the following conditions:

Email contains “@” sign;
Email contains at least one character before the “@” sign;
Email contains a domain after the “@” sign, consisting of at least 1 character before the dot, the dot itself, and at least 2 characters after the dot;
The password is at least 1 character long.

After all the checks are completed, an account is returned, or a validation error. The data types that make up our domain are very simple to describe:

interface Account {
  readonly email: string;
  readonly password: string;
}

class AtSignMissingError extends Error { }
class LocalPartMissingError extends Error { }
class ImproperDomainError extends Error { }
class EmptyPasswordError extends Error { }

type AppError =
  | AtSignMissingError
  | LocalPartMissingError
  | ImproperDomainError
  | EmptyPasswordError;

Imperatively this logic could be written as following:

const validateAtSign = (email: string): string => {
  if (!email.includes('@')) {
    throw new AtSignMissingError('Email must contain "@" sign');
  }
  return email;
};
const validateAddress = (email: string): string => {
  if (email.split('@')[0]?.length === 0) {
    throw new LocalPartMissingError('Email local-part must be present');
  }
  return email;
};
const validateDomain = (email: string): string => {
  if (!/\w+\.\w{2,}/ui.test(email.split('@')[1])) {
    throw new ImproperDomainError('Email domain must be in form "example.tld"');
  }
  return email;
};
const validatePassword = (pwd: string): string => {
  if (pwd.length === 0) {
    throw new EmptyPasswordError('Password must not be empty');
  }
  return pwd;
};

const handler = (email: string, pwd: string): Account => {
  const validatedEmail = validateDomain(validateAddress(validateAtSign(email)));
  const validatedPwd = validatePassword(pwd);

  return {
    email: validatedEmail,
    password: validatedPwd,
  };
};

All these function signatures share the same charateristic I’ve mentioned in the beginning — they don’t signalise for the user of such API that they throw exceptions. Let’s rewrite this code in a functional style using Either:

import { pipe } from 'fp-ts/function';
import { either as E, nonEmptyArray as A } from 'fp-ts';
import Either = E.Either;

Rewriting imperative code which throws exceptions into code with Eithers is simple enough — in all places, where you see a throw statement, return Left value:

// Was:
const validateAtSign = (email: string): string => {
  if (!email.includes('@')) {
    throw new AtSignMissingError('Email must contain "@" sign');
  }
  return email;
};

// Became:
const validateAtSign = (email: string): Either<AtSignMissingError, string> => {
  if (!email.includes('@')) {
    return E.left(new AtSignMissingError('Email must contain "@" sign'));
  }
  return E.right(email);
};

// After simplification using ternary operator and inverting the condition:
const validateAtSign = (email: string): Either<AtSignMissingError, string> =>
  email.includes('@') ?
    E.right(email) :
    E.left(new AtSignMissingError('Email must contain "@" sign'));

All other functions are rewritten in the same way:

const validateAddress = (email: string): Either<LocalPartMissingError, string> =>
  email.split('@')[0]?.length > 0 ?
    E.right(email) :
    E.left(new LocalPartMissingError('Email local-part must be present'));

const validateDomain = (email: string): Either<ImproperDomainError, string> =>
  /\w+\.\w{2,}/ui.test(email.split('@')[1]) ?
    E.right(email) :
    E.left(new ImproperDomainError('Email domain must be in form "example.tld"'));

const validatePassword = (pwd: string): Either<EmptyPasswordError, string> =>
  pwd.length > 0 ? 
    E.right(pwd) : 
    E.left(new EmptyPasswordError('Password must not be empty'));

Finally we need to put everything together in the handler function. To do this, I will use the chainW function — this is the chain function from the monad interface that can do type widening. In general, it makes sense to tell a little about the function naming convention adopted in fp-ts:

Suffix W means type Widening. Thanks to this, it is possible to put functions that return different types in the left parts of Either/TaskEither/ReaderTaskEither and other structures based on sum types in one chain:

  // Consider types A, B, C, D, and errors E1, E2, E3, 
  // and functions foo, bar, baz working with them:
  declare const foo: (a: A) => Either<E1, B>
  declare const bar: (b: B) => Either<E2, C>
  declare const baz: (c: C) => Either<E3, D>
  declare const a: A;
  // Won't compile, because chain expect monomorphic in the left part Either:
  const willFail = pipe(
    foo(a),
    E.chain(bar),
    E.chain(baz)
  );

  // Will compile correctly:
  const willSucceed = pipe(
    foo(a),
    E.chainW(bar),
    E.chainW(baz)
  );

Suffix T can mean two things — either Tuple (for example, like in sequenceT function), or monad transformers (like in modules EitherT, OptionT and so on).
Suffix S means structure — for example, in functions traverseS and sequenceS, which accept an object in format “key — transformation function”.
Suffix L used to mean lazy, but in the recent releases it was dropped in favour of laziness by default.

These suffixes can be combined — for example, as in the apSW function: this is the ap function from the Apply type class, which can do type widening and takes a structure as input, and iterates over its keys.

Let’ sget back to writing handler. I will use chainW to collect possible errors as a sum type AppError:

const handler = (email: string, pwd: string): Either<AppError, Account> => pipe(
  validateAtSign(email),
  E.chainW(validateAddress),
  E.chainW(validateDomain),
  E.chainW(validEmail => pipe(
    validatePassword(pwd),
    E.map(validPwd => ({ email: validEmail, password: validPwd })),
  )),
);

What did we get as a result of this rewriting? First, the handler function explicitly reports its side effects — it can not only return an object of type Account, but also can return errors of the AtSignMissingError, LocalPartMissingError, ImproperDomainError, EmptyPasswordError types. Secondly, the handler function has become cleaner — the Either is just a value that does not contain any additional logic bound to it directly, so you can work with it without fear that something bad will happen at the call site.

N.B. Of course, this is just an agreement. TypeScript as a language and JavaScript as a runtime do not restrict us in any way from writing code like this:
const bad = (cond: boolean): Either<never, string> => {
  if (!cond) {
    throw new Error('COND MUST BE TRUE!!!');
  }
  return E.right('Yay, it is true!');
};
It is clear that such code is meant to be rewritten using safe methods and combinators. For example, if you work with third-party synchronous functions, they should be wrapped in Either/IOEither using the tryCatch combinator, if with promises — using TaskEither.tryCatch, and so on.

The imperative and functional examples share one flaw — they both report only the first error they encounter. The same separation of data structure behavior from business logic, which I wrote about in the section about Option, will allow us to write a version of the program that collects all errors with minimal effort. To do this, you will need to become familiar with some new concepts.

Either has a twin brother — Validation. This is exactly the same sum type, in which the right side means success, and the left side means a validation error. The nuance is that Validation requires that the operation concat :: (a: E, b: E) => E from the Semigroup typeclass was defined for the left side of type E. This allows using Validation instead of Either in tasks where it’s necessary to collect all possible errors. For example, we can rewrite the previous example (the handler function) to collect all possible input validation errors without rewriting the rest of the validation functions (validateAtSign, validateAddress, validateDomain, validatePassword).

A few words about algebraic structures which can combine two elements

Such structures form a hierarchy:

Magma, or groupoid — basic type class which defines an operation concat :: (a: A, b: A) => A. This operation is not restricted.
If we add associativity restriction for concat, we’ll get a Semigroup. In real usage they are more useful than magmas, as most of the times we have to deal with structures having significant element order — like arrays of trees.
If we add a unit (value which can be summoned out of thin air) to semigroup, we’ll get a Monoid.
Finally, if we add an inverse :: (a: A) => A operation, which allows getting an inverse for an arbitrary value, we’ll get Group.

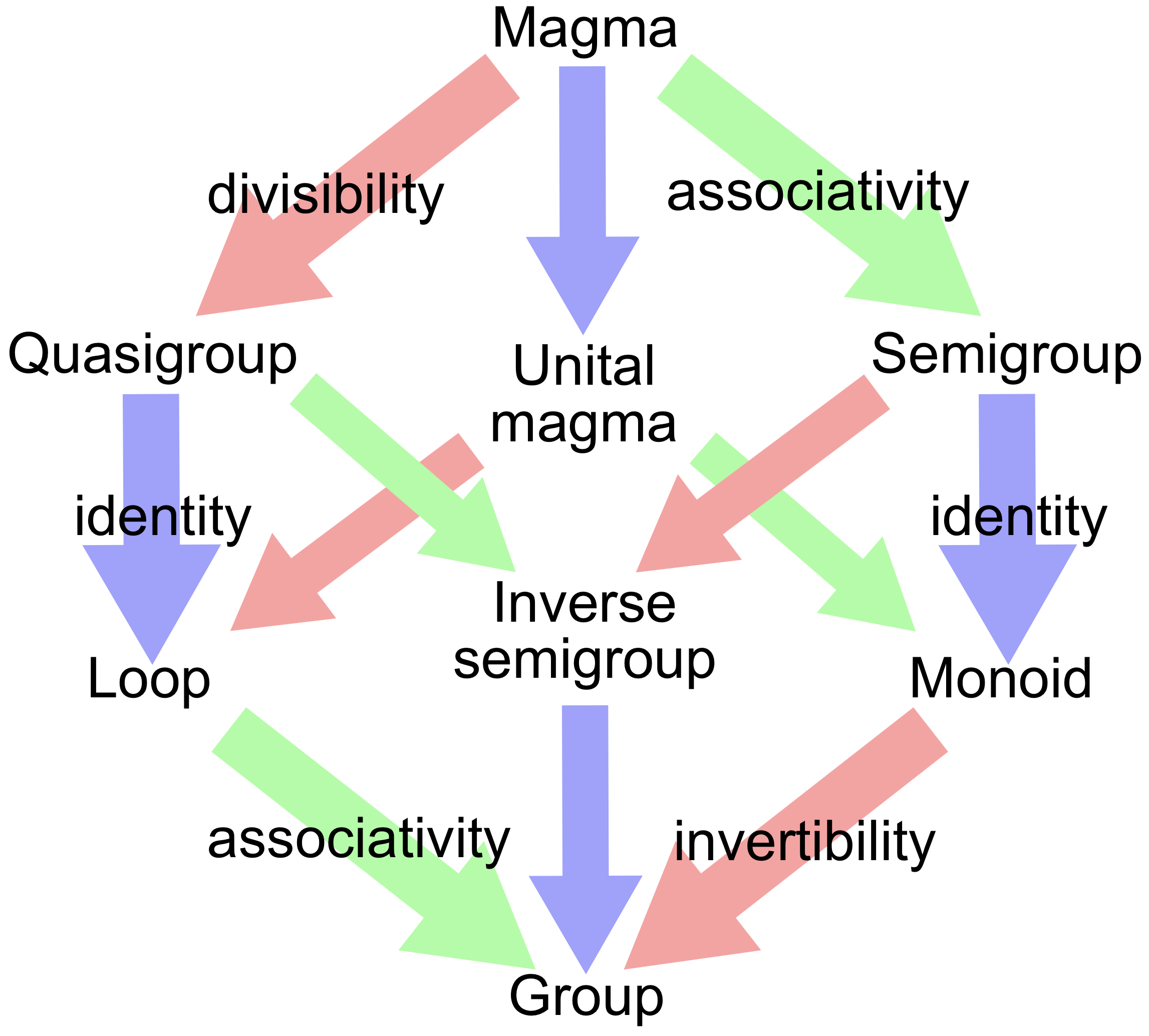Groupoid hierarchy You can read in the Wiki more details about group hierarchy.

The hierarchy of the type classes corresponding to such algebraic structures can continue: Semiring, Ring, HeytingAlgebra, BooleanAlgebra, various sorts of lattice are defined in the fp-ts library.

To solve the task of obtaining a list of all validation errors, you will need two things: the NonEmptyArray type and a Semigroup that can be defined for this type. First, let’s write a helper lift, which will translate the function of the type A => Either<E, B> into A => Either<NonEmptyArray<E>, B>:

const lift = <Err, Res>(check: (a: Res) => Either<Err, Res>) => (a: Res): Either<NonEmptyArray<Err>, Res> => pipe(
  check(a),
  E.mapLeft(e => [e]),
);

In order to collect all errors in a big tuple, I will use sequenceT from fp-ts/Apply module:

import { apply } from 'fp-ts';
import NonEmptyArray = A.NonEmptyArray;

const NonEmptyArraySemigroup = A.getSemigroup<AppError>();
const ValidationApplicative = E.getApplicativeValidation(NonEmptyArraySemigroup);

const collectAllErrors = apply.sequenceT(ValidationApplicative);

const handlerAllErrors = (email: string, password: string): Either<NonEmptyArray<AppError>, Account> => pipe(
  collectAllErrors(
    lift(validateAtSign)(email),
    lift(validateAddress)(email),
    lift(validateDomain)(email),
    lift(validatePassword)(password),
  ),
  E.map(() => ({ email, password })),
);

If we execute both handler and handlerAllErrors with an incorrect example containing more than one error, we’ll get diferent behaviour:

> handler('user@host.tld', '123')
{ _tag: 'Right', right: { email: 'user@host.tld', password: '123' } }

> handlerAllErrors('user@host.tld', '123')
{ _tag: 'Right', right: { email: 'user@host.tld', password: '123' } }

> handler('user_host', '')
{ _tag: 'Left', left: AtSignMissingError: Email must contain "@" sign }

> handlerAllErrors('user_host', '')
{
  _tag: 'Left',
  left: [
    AtSignMissingError: Email must contain "@" sign,
    ImproperDomainError: Email domain must be in form "example.tld",
    EmptyPasswordError: Password must not be empty
  ]
}

In these examples, I want to draw your attention to the fact that we receive different processing behaviour of the functions that make up the backbone of our business logic without affecting the validation functions themselves (that is, the business logic itself). In my opinion, the functional paradigm means satisfying complex requirements using simple building blocks without refactoring all parts of the system.

In the next article we will talk about Task, TaskEither and ReaderTaskEither. They will allow us to approach the idea of algebraic effects and understand what it gives us in terms of ease of development.

28 Feb 2021

« Intro to fp-ts, part 2: Type Class Pattern Intro to fp-ts, part 4: Tasks as an alternative to Promises »

Intro to fp-ts, part 3: Option and Either

Option<A> — a replacement for nullable types

Either<E, A> — computations that can diverge

A few words about algebraic structures which can combine two elements

`Option<A>` — a replacement for nullable types

`Either<E, A>` — computations that can diverge